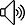題意: 求一條直線分凸包兩邊的面積。
解法: 因?yàn)轭}意會說一定穿過,那么不會有直線與某條邊重合的情況。我們只要找到一個(gè)直線分成的凸包即可,另一個(gè)的面積等于總面積減去那個(gè)的面積。
怎么得到分成的一個(gè)凸包呢?
從0~n掃過去,如果掃到的邊與直線不相交,那么把端點(diǎn)加進(jìn)新凸包中,如果直線與掃到的邊相交了,那么就將交點(diǎn)加入新凸包,然后以后不相交的話也不加入點(diǎn)到新凸包中,直到遇到下一個(gè)與直線相交的邊,則把交點(diǎn)又加入新凸包,然后在掃到末尾加入點(diǎn)。這樣就得到了。
即找到如圖:

注意四舍五入。
代碼:

#include <iostream>
#include
<cstdio>
#include
<cstring>
#include
<cstdlib>
#include
<cmath>
#include
<algorithm>
#define
eps 1e-8
using
namespace
std;
struct
Point{
double
x,y;
Point(
double
x=
0
,
double
y=
0
):x(x),y(y) {}
void
input() { scanf(
"
%lf%lf
"
,&x,&
y); }
};
typedef Point Vector;
int
dcmp(
double
x) {
if
(x < -eps)
return
-
1
;
if
(x > eps)
return
1
;
return
0
;
}
template
<
class
T> T sqr(T x) {
return
x *
x;}
Vector
operator
+ (Vector A, Vector B) {
return
Vector(A.x + B.x, A.y +
B.y); }
Vector
operator
- (Vector A, Vector B) {
return
Vector(A.x - B.x, A.y -
B.y); }
Vector
operator
* (Vector A,
double
p) {
return
Vector(A.x*p, A.y*
p); }
Vector
operator
/ (Vector A,
double
p) {
return
Vector(A.x/p, A.y/
p); }
bool
operator
< (
const
Point& a,
const
Point& b) {
return
a.x < b.x || (a.x == b.x && a.y <
b.y); }
bool
operator
>= (
const
Point& a,
const
Point& b) {
return
a.x >= b.x && a.y >=
b.y; }
bool
operator
<= (
const
Point& a,
const
Point& b) {
return
a.x <= b.x && a.y <=
b.y; }
bool
operator
== (
const
Point& a,
const
Point& b) {
return
dcmp(a.x-b.x) ==
0
&& dcmp(a.y-b.y) ==
0
; }
double
Dot(Vector A, Vector B) {
return
A.x*B.x + A.y*
B.y; }
double
Length(Vector A) {
return
sqrt(Dot(A, A)); }
double
Cross(Vector A, Vector B) {
return
A.x*B.y - A.y*
B.x; }
Point DisP(Point A,Point B) {
return
Length(B-
A); }
bool
SegmentIntersection(Point A,Point B,Point C,Point D) {
return
max(A.x,B.x) >= min(C.x,D.x) &&
max(C.x,D.x)
>= min(A.x,B.x) &&
max(A.y,B.y)
>= min(C.y,D.y) &&
max(C.y,D.y)
>= min(A.y,B.y) &&
dcmp(Cross(C
-A,B-A)*Cross(D-A,B-A)) <=
0
&&
dcmp(Cross(A
-C,D-C)*Cross(B-C,D-C)) <=
0
;
}
void
SegIntersectionPoint(Point& P,Point a,Point b,Point c,Point d) {
//
需保證ab,cd相交
P.x = (Cross(d-a,b-a)*c.x - Cross(c-a,b-a)*d.x)/(Cross(d-a,b-a)-Cross(c-a,b-
a));
P.y
= (Cross(d-a,b-a)*c.y - Cross(c-a,b-a)*d.y)/(Cross(d-a,b-a)-Cross(c-a,b-
a));
}
double
CalcConvexArea(Point* p,
int
n)
{
double
area =
0.0
;
for
(
int
i=
1
;i<n-
1
;i++
)
area
+= Cross(p[i]-p[
0
],p[i+
1
]-p[
0
]);
return
fabs(area*
0.5
);
}
Point p[
25
],ch[
25
];
Point P,A,B;
int
main()
{
int
n,i,m;
while
(scanf(
"
%d
"
,&n)!=EOF &&
n)
{
for
(i=
0
;i<n;i++
) p[i].input();
A.input(), B.input();
Point tmpA
= B+(A-B)*
20003
, tmpB = A+(B-A)*
20003
;
A
= tmpA, B =
tmpB;
double
Total =
CalcConvexArea(p,n);
int
tot =
0
, fir =
0
, add =
0
;
ch[tot
++] = p[
0
];
for
(i=
0
;i<n;i++
)
{
Point C
= p[i], D = p[(i+
1
)%
n];
if
(SegmentIntersection(A,B,C,D))
{
SegIntersectionPoint(P,A,B,C,D);
ch[tot
++] =
P;
if
(!fir) fir =
1
;
else
fir =
0
, add =
1
;
if
(P == D) i++
;
}
else
if
(!fir) ch[tot++] = p[(i+
1
)%
n];
if
(add) ch[tot++] = p[(i+
1
)%
n];
}
double
Now =
CalcConvexArea(ch,tot);
double
Other = Total-
Now;
int
N = (
int
)(Now+
0.5
), O = (
int
)(Other+
0.5
);
if
(O >
N) swap(N,O);
printf(
"
%d %d\n
"
,N,O);
}
return
0
;
}
?
更多文章、技術(shù)交流、商務(wù)合作、聯(lián)系博主
微信掃碼或搜索:z360901061

微信掃一掃加我為好友
QQ號聯(lián)系: 360901061
您的支持是博主寫作最大的動力,如果您喜歡我的文章,感覺我的文章對您有幫助,請用微信掃描下面二維碼支持博主2元、5元、10元、20元等您想捐的金額吧,狠狠點(diǎn)擊下面給點(diǎn)支持吧,站長非常感激您!手機(jī)微信長按不能支付解決辦法:請將微信支付二維碼保存到相冊,切換到微信,然后點(diǎn)擊微信右上角掃一掃功能,選擇支付二維碼完成支付。
【本文對您有幫助就好】元